Ensuring the safety and reliability of advanced algorithms that control many complex systems such as self-driving cars or robots is an ongoing challenge, especially as these systems are deployed in increasingly diverse environments.
To address this challenge, engineers at Johns Hopkins University have developed a novel method that combines artificial intelligence—specifically neural networks—with advanced mathematical techniques to create more reliable control systems for complex machines. Their results appear in IEEE Control Systems and Letters.
“By using advanced AI techniques with a principled mathematical framework, we’ve significantly improved the stability and reliability of automated systems. This advancement could lead to the development of more dependable robots and autonomous vehicles that can safely operate under a broad range of conditions,” said Jiarui Wang, MS ’23, who worked with Mahyar Fazlyab, an assistant professor of electrical and computer engineering and instructor in the Whiting School of Engineering’s Engineering for Professionals’ ECE program, on the study.
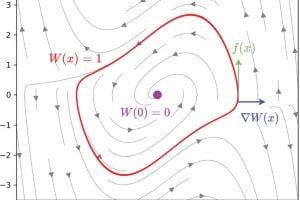
Wang said one key goal was to expand what’s known as the “region of attraction” (RoA): The range of states from which the control system is guaranteed to be able to stabilize the machine.
To this end, Wang and Fazlyab combined neural networks with a mathematical tool called Zubov’s Partial Differential Equation (PDE). This approach allows for precise mapping of the RoA’s boundaries, providing a clearer understanding of where a control system is effective and under what conditions it might fail.
“Our approach combines the Zubov PDE with actor-critic framework in deep reinforcement learning which contains two neural networks,” said Wang. “One neural network – the actor – learns to control the robot while the other – the critic – is trained with the Zubov PDE to predict how far the machine is from stabilization. This collaboration allows us to improve and evaluate the controller jointly.”
The researchers say their approach thus ensures that the neural networks not only keep the machine stable but also maximize the area where this stability holds true.
“What set this approach apart is that it combines the Zubov PDE from control theory, physics-informed neural networks—which is a modern method to numerically solve PDEs—and the actor-critic framework from modern reinforcement learning,” said Fazlyab. “This means we can accurately characterize the RoA and effectively learn the controller at the same time”
In practical tests across different scenarios, their method consistently increased the size of the RoA compared to traditional methods. This means the control systems could maintain stability over a larger range of conditions, making them more reliable and robust in real-world applications, they say.
Wang and Fazlyab say they plan to apply their method to even more complex systems, ensuring that these control systems remain resilient against unexpected changes or errors in real-world dynamics. They believe this could lead to safer and more efficient technologies across industries, from robotics to autonomous vehicles.