In our approach, the governing equations are solved using the so-called one- fluid or one-field formulation, where a single set of equations is written for the whole computational domain and the different fluids and phases are identified by an index function. For two fluids, the index function is usually one in one fluid and zero in the other. For additional phases the index function can either take other values, or additional index functions can be used. The index function is used to set the material properties of each fluid, which are generally constant in each one (although that is not necessary), changing abruptly at the fluid-fluid interfaces. Physical effects confined to the interface, such as surface tension or release of latent heat are added as singular terms to the governing equations. Using the one-fluid formulations allows the governing equations to be solved on fixed structured grids. Its use goes back to the beginning of computational fluid dynamics and most numerical approaches to simulations of multi- phase flows are based on it. The discontinuous index function is advected by the flow and in many methods, such as volume-of-fluid and level set methods the index function is advecteddirectly on the grid. While this approach often produce high quality solutions, maintaining the integrity of the interface and finding the surface tension at the interface can be a challenge, particularly for resolved.
Our strategy is different and we use connected marker points, forming a moves with the flow, to identify the interface and find surface tension and the index function from the location of the grid. The Figure shows the basic elements of the method.
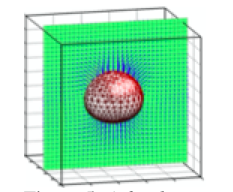
Figure: A fixed structured grid is used to solve the governing equations and a triangulated un- structured grid to track the interface.
This hybrid approach, solving the governing equation on a fixed (Eularian) grid and following the interface using a moving (Lagrangian) grid combines the best features of the different strategies and results in an accurate and versatile method that has been used to simulate a large number of multifluid and multiphase problems. This approach also results in a relatively simple code. The governing equations are solved in a similar way as in other approaches (VOF and LS, for example) and in our case we generally use a finite volume method where high order upwind schemes are used for the advection terms and centered approximations for the viscous/diffusion terms. For incompressible flows the pressure equation is solved by advanced methods such as the Krylov solvers in HYPRE. The velocity of the interface markers is interpolated from the fixed flow grid. As the interface deforms, marker points are dynamically added and deleted to maintain adequate resolution of the interface. In some cases, the interface topology is also modified to accommodate coalescence and breakup of fluid masses. The method was originally introduced in Unverdi & Tryggvason; (1992) and various refinements and extensions are described in Tryggvason et al. (2011). It has been used to examine a large number of problems and tested in various ways to demonstrate its convergence and accuracy, as discussed above.
References
S. O. Unverdi and G. Tryggvason. A front-tracking method for viscous, incompressible, multi-fluid flows. Journal of Computational Physics, 100:25–37, 1992.
G. Tryggvason, R. Scardovelli, and S. Zaleski. Direct Numerical Simulations of Gas-Liquid Multi- phase Flows. Cambridge University Press, 2011.