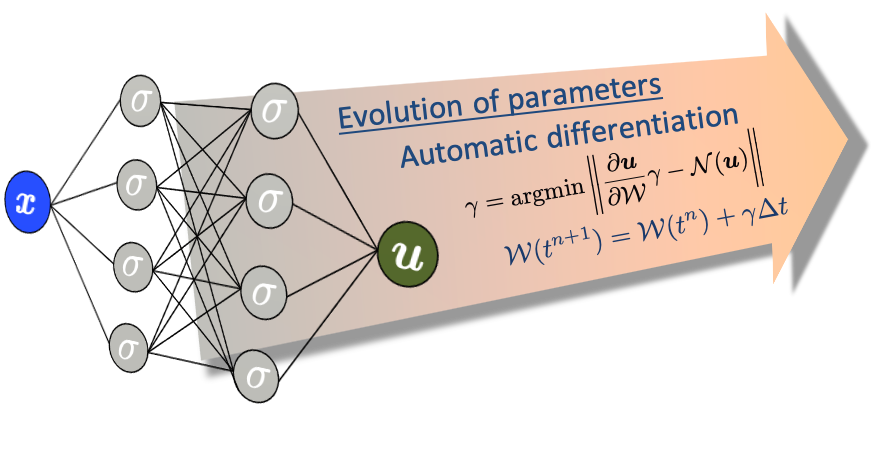
Evolutional Deep Neural Networks (EDNN) are a powerful new approach to solving partial differential equations (PDE). The parameters of the network are trained to represent the initial state of the system only, and are subsequently updated dynamically, without any further training, to provide an accurate prediction of the evolution of the PDE system. In this framework, the network parameters are updated dynamically, using the governing equations. As such, the predictions accurately satisfy the governing equations, and trajectories can be evolved for indefinitely long times, which is not feasible for other neural network approaches.
EDNN was invented by our research group (Du & Zaki, Phys. Review E 2021). Its versatility, accuracy and predictive capabilities have been demonstrated for a wide range of applications including the heat transfer, nonlinear advection, chaotic dynamics and turbulent flows.
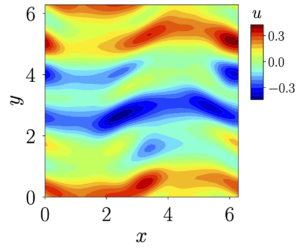
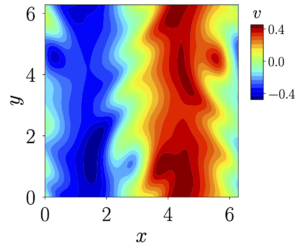
Current applications of EDNN include predictions of flows around bluff bodies, transition to turbulence, and viscoelastic flows. And example is shown below where EDNN was used to solve the evolution of Kolmogorov flow, which starts from a laminar initial state and transition to chaotic dynamics.