Create
Design Project Gallery
Uniformly Faster Gradient Descent of Varying Step Sizes for Smooth Convex Functions
- Program: Applied Mathematics and Statistics
- Course: Other
- Year: 2025
Project Description:
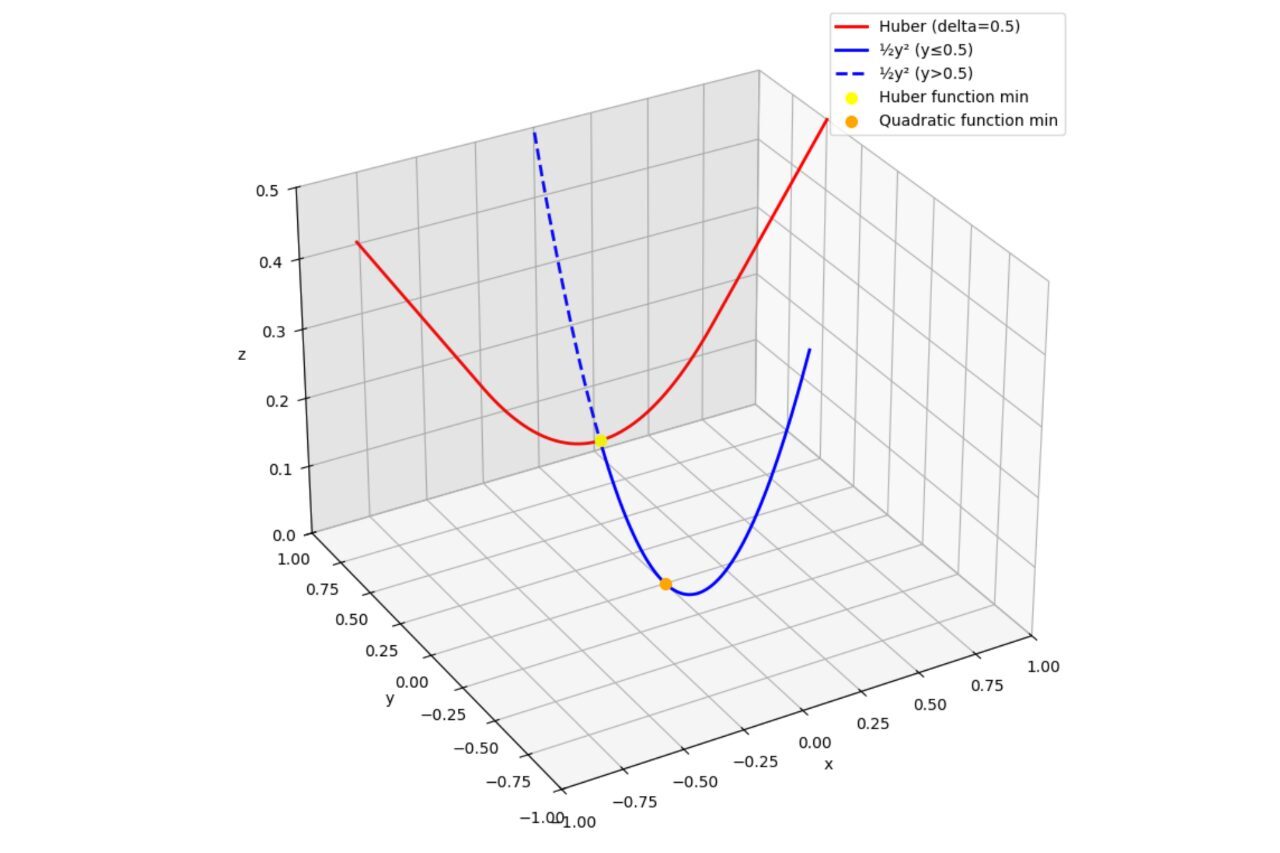
Recent literature has discovered a fixed Silver step size schedule with occasional long steps for gradient descent which achieves an accelerated overall convergence guarantee on smooth convex functions. The problem with the Silver steps is that acceleration is only guaranteed at designated stopping points in the schedule. Our project seeks to address the open question of whether there exists a fixed schedule that achieves acceleration when stopping anywhere during the schedule. We first hypothesized that the improved step size schedule does not exist, based on evidence from numerical experiments using Performance Estimation Problems (PEP) software. Next, we employed proof techniques, including using Huber function and half quadratic function, as well as induction to try to prove the null result that a schedule with an accelerated anytime guarantee does not exist.
Project Photo:
We hypothesize that there exists a worst-case function that prevents a schedule that achieves guarantee acceleration over than O(1/t) by using long steps. Given the oscillating nature of the approximated stepsize schedule, we try to construct such worst-case function by combining Huber and half-quadratic functions, as demonstrated in the 3D photo.