Create
Design Project Gallery
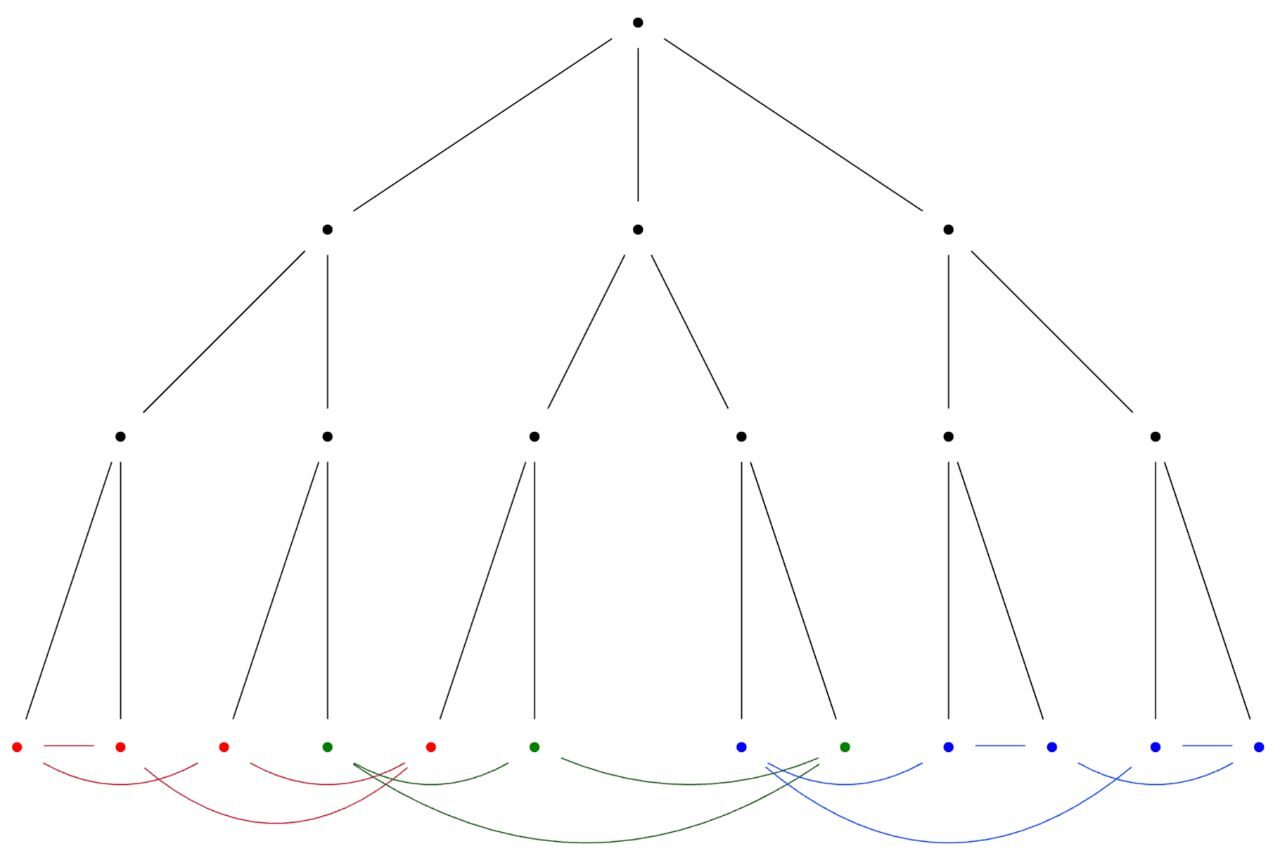
Tree Models of Random Regular Graphs
- Program: Applied Mathematics and Statistics
- Course: Other
- Year: 2025
Project Description:
Expander graphs are graphs that are simultaneously sparse and very well-connected. These graphs are useful in a wide range of applications, from generating pseudorandom numbers through random walks, to robust error-correction and channel communication. Graph connectivity is related to the spectral gap of the adjacency matrix, which motivates constructing expander graphs with maximal spectral gap, known as Ramanujan graphs.
As it turns out, random regular graphs drawn uniformly at random are already excellent expanders and, according to recent work, even often Ramanujan. They have few small cycles, locally tree-like structure, and large spectral gaps. Yet, derandomizing such constructions or replacing them with explicit graphs is an open problem.
I will present progress on a project to investigate possible new methods of generating regular graphs with expander-like properties, such as enforced tree-like configurations, and generate such expander-like graphs more easily and with higher probability.