Many complex systems can be modeled as a network of interacting subsystems, each with simple dynamics. In this work we use oscillator networks as a model of power grids and vehicular platoons. By applying tools from control theory to this modeling framework we investigate the effect of network structure on the synchronization performance of such systems. We show that for a large class of performance measures, the performance is determined by effective resistances in the underlying graphs. These results show the strong connection between the synchronization performance of oscillator networks and circuit theory. Applications include evaluating the transient resistive losses due to maintaining synchrony in power grids as well as quantifying the coherence of vehicular platoons with different control laws and communication structures.
Nodes
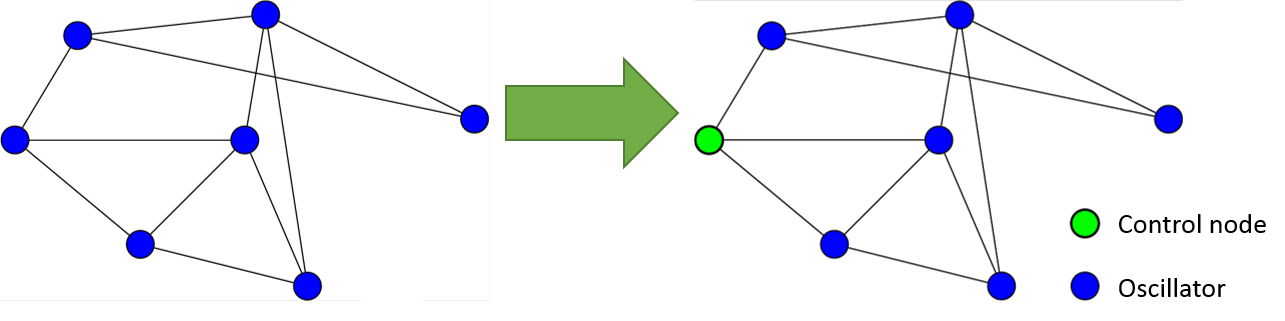
We can use oscillator networks to evaluate a network’s synchronization performance. Synchrony exists when all subsystems, or agents in a system, reach a mutual goal. To improve the performance of a network, we can tune the dynamics at particular nodes, as shown in the diagram below.
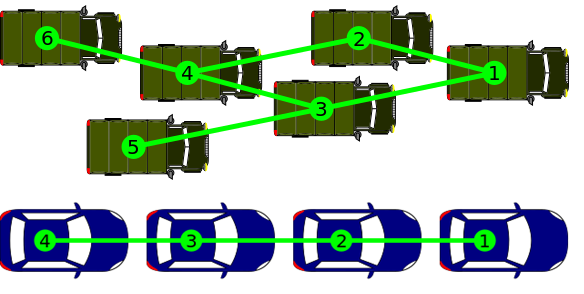
Example Network: Vehicular Platoons
In the case of vehicular platoons, synchronization would occur if the vehicles reach nominal spacing and velocity. Here, tuning the dynamics at particular nodes involves reducing communication in a vehicle platoon by tuning the leader’s dynamics.
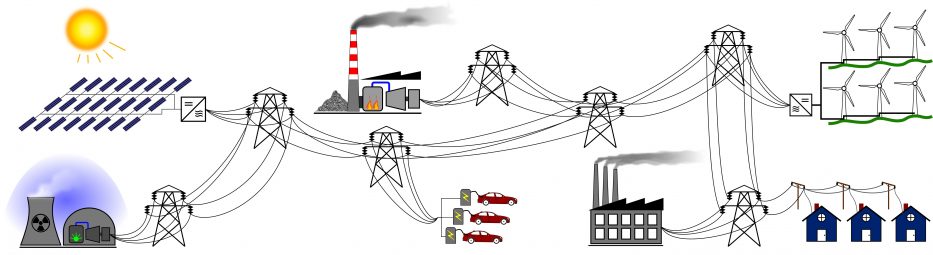
Example Network: Power Grid
In the case of power grids, synchronization is reached when all generator phases reach nominal conditions with constant angular velocities. The cost associated with resynchronization, then, would be the transient losses of energy in a power grid. We can improve the performance by tuning a droop-controlled inverter and therefore reduce the resistive losses due to maintaining synchrony. The droop-control approximates the average power versus frequency properties of a synchronous generator, but has different dynamics.